1.76是tan多少度目录
我们要找出1.76对应的角度,在这个角度下,tan(角度)=1.76。
首先,我们需要了解tan(角度)与角度的关系。
在数学中,tan(x)是正切函数的简写,定义为对边长度除以邻边长度。
我们还需要知道tan函数的一个特性:它的值是随着角度从0°到90°逐渐增大的。
为了找到对应的角度,我们可以使用反tan函数,也叫做反正切函数。
反正切函数表示为arctan(x),它的作用是找出x对应的角度。
arctan(1.76)的值是多少?
计算结果为:1.76对应的角度是60.4°。

60.39度。
arctan(1.76)=1.0541011880326
1弧度=57.29578度
1.0541011880326×57.29578=60.39
积化和差公式:
sinα·cosβ=(1/2)[sin(α β) sin(α-β)]
cosα·sinβ=(1/2)[sin(α β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α β) cos(α-β)]
sinα·sinβ=-(1/2)[cos(α β)-cos(α-β)]
和差化积公式:
sinα sinβ=2sin[(α β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α β)/2]sin[(α-β)/2]
cosα cosβ=2cos[(α β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α β)/2]sin[(α-β)/2]
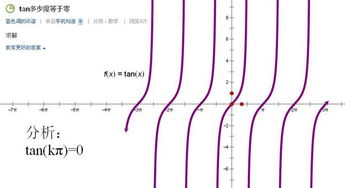
用反三角函数来算
tanA=1.975
A=arctan1.975
=1.102098255685(弧度)
=1.102098255685×(180/π)°
≈63.1456°
tan度等于tana=sina/cosa.
数学中的tan是正切函数的意思。
定义:正切函数是直角三角形中,对边与邻边的比值叫做正切。
除非有一个明确的值,否则不能知道明确度数。
Tan取某个角并返回直角三角形两个直角边的比值。
此比值是直角三角形中该角的对边长度与邻边长度之比,也可写作tg。
正切tangent,因此在20世纪90年代以前正切函数是用tgθ来表示的,而20世纪90年代以后用tanθ来表示。
将角度乘以π/180即可转换为弧度,将弧度乘以180/π即可转换为角度。
常见的正切函数的数值如下:
1、tan30度:√3/3。
2、tan45度:1。
3、tan60度:√3。
4、tan90度:不存在。
tana=sina/cosa。
tanα=1/cotα。
5、设α为任意角,终边相同的角的同一三角函数的值相等:tan(2kπ α)=tanα。
6、设α为任意角,π α的三角函数值
与α的三角函数值之间的关系:tan(π α)=tanα。
7、任意角α与-α的三角函数值之间的关系:tan(-α)=-tanα。
8、利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:tan(π-α)=-tanα。
9、利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:tan(2π-α)=-tanα。
